Two algorithms make use of quantum mechanics in order to beat classical algorithm performances: Shore’s and Grover’s algorithms. We have chosen to implement the latter, which is a search algorithm to find an element in an unsorted list of elements. Grover showed that his quantum algorithm can find an element in a time proportional to sqrt(N), where N is the total number of elements. A classical algorithm would need a time proportional to N. We decided to make a proof-of-principle of Grover’s algorithm with a four-level nuclear spin system, following the theoretical proposal of Leuenberger and Loss [Nature 2003].
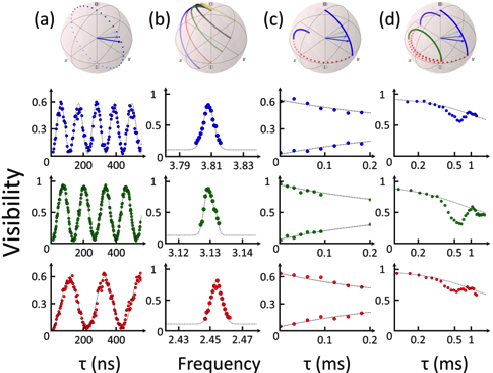Qubits coherent manipulation. The trajectory on the Bloch sphere is illustrated at the top of each graph. There is one colour per transition: 0-1, 1-2, 2-3 respectively in red green and blue a) Rabi oscillations of a single nuclear spin qubit between the four energy levels. The frequency of the Rabi oscillation can be tune from 0.5 to 5 MHz. b) Maximum visibility of the Rabi oscillation as function of detuning yields the resonance frequency. c) Maximum of the Ramsey fringes as a function of the waiting time between the two pi/2 pulses, yielding a coherence time of the order of 0.3 ms for the three transitions. d) Hahn spin-echo measurements as a function of the waiting time between the pi/2 and pi-pulse, showing that we are far from the limit T1=2*T2. This indicate that the decoherence mechanism is not due to relaxation process.
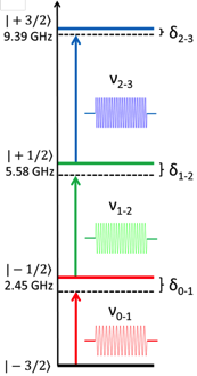
(Left) Implementation of Grover’s algorithm into the energy diagram of the Terbium four nuclear spin states. A quadrupole component in the hyperfine coupling enables an independent manipulation of each transition. We define the frequency of the microwave pulse ωn-m that drive the (n-m) transition and the detuning δn-m between the transition and microwave pulse frequency.
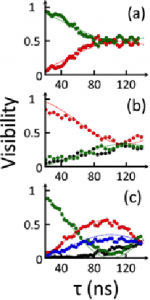
(Right) Realisation of the Hadamard gate for (a) 2, (b) 3 and (c) 4 nuclear spin states. Evolution of the nuclear spin states population as a function of the microwaves pulse length is plotted. The colour code is the one of Fig. 4. The superposition state with the same phase is reached after about 110 ns for (a) and (b).